Problema matemático del confinamiento 23. Una paradoja y dos problemas de lógica común y familiar.

Siguiendo con actividades de lógica voy a proponer una paradoja muy interesante, a base de tres sentencias claras:

1. Este libro tiene 597 páginas.

2. El autor de este libro es Confucio.
3. Las frases 1, 2 y 3 son falsas.

Esta paradoja fue recogida en Kasner, E. y Newman, J. R. (1956). Paradoja perdida y paradoja recuperada. En J. R. Newman Sigma. El mundo de las Matemáticas 5. Ed. Grijalbo, Barcelona. P. 323 – 341.

Y dos problemas de lógica común y familiar, muy sencillos:

“Los dos etíopes.

Dos etíopes entran en un bar; uno de los etíopes es padres del hijo de su acompañante. ¿Cuál es su parentesco?”

“La familia.

Señalando a uno de los retratos familiares de la galería, aquel hombre observó: ‘No tengo hermanos ni hermanas, pero el padre de ese hombre es el hijo de mi padre’. ¿Qué parentesco había entre quien hablaba y la persona del retrato?”

Estos dos problemas aparecen en el libro de I. Morris (1973). Tres sombras en el camino. Y otros rompecabezas mentales. Paneuropea de Ediciones y Publicaciones, S. A. Barcelona.

Les Luthiers y el Teorema de Tales. Ha fallecido Marcos Mundstock.

Ha fallecido Marcos Mundstock, una de las caras más visibles de Les Luthiers.

Nos compramos su disco allá por los años setenta y, desde entonces, hemos seguid su trayectoria y asistido a algunos de sus conciertos en directo. Siempre magníficos en la música y en el humor.

Les Luthiers y el teorema de Tales

Hoy en homenaje a Marcos Mundstock y a su grupo sustituimos el problema matemático del confinamiento por este video en el que escucharemos “El Teorema de Tales”, que el compositor Johan Sebastian Mastropiero dedicó a la condesa de Shortshot.

La voz de Les Luthiers HOY (23/04/2020)

Problema matemático del confinamiento 22. Otra paradoja similar a la anterior, al girar una moneda sobre otra.

“Cogemos dos monedas idénticas de tamaño y las situamos una junto a otra como se muestra en la figura 1.
Hacemos girar la primera sobre la segunda una semicircunferencia, hasta alcanzar el otro lado, según la posición de la figura 2.
Como la moneda solo ha girado una semicircunferencia podríamos esperar que la figura estuviera invertida. Pero, la posición de la moneda es como si hubiera girado completamente alrededor de su propia circunferencia.”

La monedad, a pesar de girar una semicircunferencia, da la vuelta completa.

Es posible que alguien pueda decir como algunos alumnos me decía cuando les mostraba estas situaciones: “Esos son cosas de las matemáticas”.

Kasner, E. y Newman, J. R. (1956). Paradoja perdida y paradoja recuperada. En J. R. Newman Sigma. El mundo de las Matemáticas 5. Ed. Grijalbo, Barcelona. P. 323 – 341.

Como pista, aunque muchos no la necesitarán.

Problema matemático del confinamiento 21. Una paradoja. ¿Pueden dos circunferencias de diferente radio tener la misma longitud?

Hoy retomamos las paradojas y la bibliografía. Así he retomado una paradoja que ilustro con las referencias de E. Kasner y J. R. Newman (1956), que vemos en la figura.

"Dos circunferencias concéntricas dan la vuelta completa al rodar de A a B, por lo que la distancia AB es igual que la longitud de la circunferencia mayor. La circunferencia interior (y menor) también da una vuelta completa al ir desde C a D. Los segmentos AB y CD son iguales y representan, respectivamente, las longitudes de la circunferencia exterior e interior. Consecuentemente, llegamos a que las longitudes de las circunferencias exterior e interior son iguales."

Kasner, E. y Newman, J. R. (1956).

Kasner, E. y Newman, J. R. (1956). Paradoja perdida y paradoja recuperada. En J. R. Newman Sigma. El mundo de las Matemáticas 5. Ed. Grijalbo, Barcelona. P. 323 – 341. 

La de mañana será otras paradoja similar y aportaré la solución,

Problema matemático del confinamiento 20. Qui trouve ceci? ¿Quién soluciona esto?

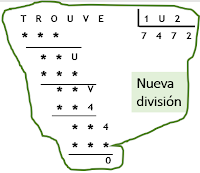
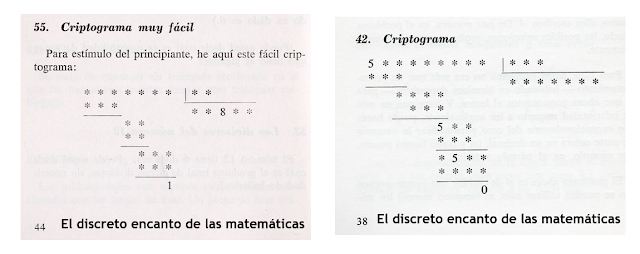
El título de esta actividad encontrada en el El discreto encanto de las matemáticas (M. Matáix, 1981) me ha sugerido proponerla de manera específica y mostrar que tiene solución, que para unos sencilla y para otros complicada.

Como es la solución de este problema del confinamiento que nos toca ahora vivir.

Evidentemente, para resolver este problema implica conocer el algoritmo de la división, propio de los niveles de primaria. Sugerimos repasar el algoritmo mostrado siguiendo la rutina y anotar aquellos pasos que nos dan alguna pista sobre los posibles números.

Así, observando el algoritmo vemos que C x QUI = _*** ; E x QUI = _*** ; C x QUI = _**E ; I x QUI = _***

En tercer producto (C x QUI = _**E) nos indica que C x I acaba en E. El producto final de I x I = I² tiene que terminar en E para que la resta final sea cero. A partir de aquí vemos los números que cumplen estas dos observaciones.

Destacamos los casos que cumplen que I² = termina en E, pero puede ser un número de una o dos cifras.

(I = 2; E = 4) (I = 3; E = 9) (I = 4; E = 6) (I = 7; E = 9) (I = 8; E = 4) (I = 9; E = 1). En los demás casos coincidiría el valor de las dos letras.

Recordamos que C X I acaba en E y analizamos los casos anteriores:

 (I = 2; E = 4) C podría valer 7, ya que 7 x 2 = 14

(I = 4; E = 6) C podría valer 9, ya que 9 x 4 = 36; (I = 8; E = 4) C podría valer 3, ya que 3 x 8 = 24

En los demás casos, (I = 3; E = 9) (I = 7; E = 9) (I = 9; E = 1) no es posible

Por lo tanto, quedan tres posibilidades (I = 2; E = 4; C = 7) (I = 4; E = 6; C = 9) (I = 8; E = 4; C = 3). Consideramos la primera.

Si (I = 2; E = 4; C = 7) y C x QUI = _*** con solo tres números significa que C x Q más lo que puedas llevarte es menos que T. Entonces, Q = 1; y T sólo puede valer 7, 8 ó 9.

Sustituyendo C, E, I, Q en el algoritmo mostrado, tenemos una nueva representación, que analizamos siguiendo los pasos de la dicición:

 

Llegado aquí, tenemos el divisor que es 132 y el cociente que es 7.472, con el resto cero.

Con una multiplicación obtenemos el dividendo 132 x 7472 = 986.304

Podemos realizar la operación completa.

AH! Pero el problema no ha terminado, quedaban otras dos ternas: (I = 4; E = 6; C = 9) y (I = 8; E = 4; C = 3), pero ya dejo al lector demostrar que estas no pueden ser y que la solución mostrada es la única.

Por supuesto, en el caso de coronavirus, como en muchos otros problemas de matemáticas puede haber varias soluciones.

Problema matemático del confinamiento 19. Un poco de lógica y exploradores de la mano de Mariano Mataix

Hoy vamos a proponer para el fin de semana dos problemas de lógica, muy sencillos.

"Verdades y mentiras.

La conocida isla de Sinó, está poblada por los Tacas, que siempre mienten, y los tiquis, que siempre dicen la verdad. Un explorador encontró a tres indígenas y les preguntó a que raza pertenecían.

El 1º contestó tan bajo que el explorador no oyó.

El 2º dijo, señalando al primero: “Ha dicho que es un taca”

El 3º, interpretó al 2º: “¡Tú eres un mentirosos!”. De que raza era este tercer indígena?".

(M. Mataix (1981). El discreto encanto de las matemáticas. Marcombo. Barcelona. P. 24.

 "Travesía del desierto con porteadores.

¿Cuántos porteadores necesitará un explorador para hacer un viaje de seis días a través del desierto, si cada persona puede llevar alimentos y bebida para abastecerse durante cuatro día? ¿Cuál será el número mínimo de porteadores?" (M. Mataix (1981). El discreto encanto de las matemáticas. Marcombo. Barcelona. P. 22.

Problema matemático del confinamiento 18. Jugando con los algoritmos de operaciones de la aritmética elemental - 2

En homenaje a Mariano Mataix voy a dar continuidad a sus criptogramas elementales. Mostraré cinco de los muchos que propuso en sus numerosos libros. Algunos fueron muy populares como el "send more money" y otros son un poco más complicados de resolver.

Problema matemático del confinamiento 17. Jugando con los algoritmos de operaciones de la aritmética elemental - 1

L. J. Blanco. Clasificación de Problemas

Importante para el cálculo aritmético es la automatización del procedimiento y la comprensión de los sucesivos pasos que se siguen en los algoritmos.

M. Mataix (1981). p. 22

En Blanco (1993a y 1993b) se indica que “para este tipo de actividades la matemática recreativa nos sugiere algunos ejemplos que, al mismo tiempo que ayudan a profundizar en algún algoritmo concreto, pueden ser utilizados como ejercicios de lógica.” Mariano Mataix llamaba a estos ejercicios criptogramas elementales. A modo de ejemplo, y para el algoritmo de la multiplicación presentamos estas actividades, donde hay que sustituir los asteriscos por números del 0 al 9.

La realización de esta actividad supone trabajar el algoritmo de la multiplicación, pero de una manera diferentes y ayuda a profundizar sobre los procesos implicados en el algoritmo.

Blanco, L.J. (1993a). Consideraciones elementales sobre la resolución de problemas. Universitas Editorial. Badajoz.

Blanco, L.J. (1993b). Una clasificación de problemas matemáticos. Revista Épsilon nº 25. 49 - 60.

Mataix, M. (1981). El discreto encanto de las matemáticas. Marcombo. Barcelona.

Problemas Matemáticos del Confinamiento publicados hasta el 11 de abril de 2020.

Desde el 20 de marzo, unos días después de iniciarse el confinamiento, inicié la publicación de los Problemas Matemáticos del Confinamiento. 

Son problemas del nivel de primaria y secundaria que pueden dar juego en las aulas, para enseñar a resolver problemas.

Os dejo la relación de los 15 primeros, con los enlaces.

Problemas matemáticos del confinamiento

15. Rellenar una superficie cuadrada con círculos.
14. ¿Cuántas caras pintadas tienen los cubitos?
13. Analizamos ¿figuras equivalentes? Curiosidades del cortar y pegar.
12. Identificando conceptos geométricos en un rosetón de la Estación deEstambul.
11. Juegos de números y operaciones aritméticas y algebraicas. Hagamos nuestroscuadros mágicos.
10. Algunos relojes curiosos.
9. ¿Cuánto mide la diagonal del cuadrado?
8. No tengo tiempo para ir al colegio. No hay días en el año.
7. Valor numérico de las letras y palabras.
6. Con los nueves dígitos llegar a 100.
5. Construir los números naturales con cuatro cuatros.
4. Reparto de bocadillos y monedas.
3. Un testamento curioso y un interesante reparto.
2. Algunos problemas con sucesiones numéricas.
1. Recubrir un tablero de ajedrez con fichas de dominó.

Seguiremos hasta el final, que será cuando empecemos a analizarlos y publicar las soluciones más interesantes.

Problema matemático del confinamiento 16. El engaño en la venta de espárragos

Un problema sobre proporcionalidad con perímetros y superficies que abarcan.

Dice una vieja historia que cierto día acercose un mozo a un vendedor de espárragos en el mercado, y le dijo:

- Ved que traigo conmigo este cordel que mide un palmo, y pregunto cuánto me cobraréis por el mazo de espárragos que pueda atar con él.

Pidió el aldeano cinco reales y el mozo se mostró conforme, pagó y se llevó la mercancía.

A los dos días presentose el mozo y dijo:

Aquí vengo con este cordón que mide dos palmos. Os acordaréis que por los espárragos que pude atar con el cordel de un palmo, me cobrasteis cinco reales. Así que por el mazo que atemos con este cordón de dos palmos os pagaré diez reales, si lo veis justo.

Aceptó el aldeano, aunque le quedó cierta duda  sobre la venta.

Es un problema muy interesante ya que puede resolverse en diferentes niveles educativos a partir de la manipulación (cuerda y bolígrafos), con representaciones de figuras geométricas (papel cuadriculado y compás o hilo), el uso de expresiones aritméticas y algebraicas (con cantidades concretas o expresiones generales).