Geometría. Entrada 3.
 |
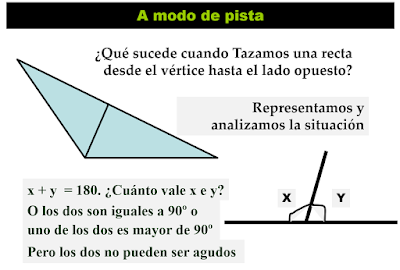
| Dividir un triángulo obtusángulo en triángulo acutángulo. |
El bloqueo ante los problemas de Matemáticas provoca,
en numerosas ocasiones, ansiedad en los resolutores. Ello les lleva al abandono y
a la generación de actitudes negativas ante la resolución de problemas.
El
bloqueo es una situación típica en los estudiantes de secundaria cuando abordan
problemas de Matemáticas. Inconscientemente, repiten una acción renunciando a otras alternativas. No es suficiente el
conocimiento de los pasos del Modelo General de Resolución de Problemas y se
requiere otras experiencias.
Si
embargo, existen sugerencias que pueden ayudarnos a salir del impasse. En
Blanco (1983) se proponen algunas de estas propuestas que se ilustran con
algunos problemas y acciones concretas para salir del bloqueo. Recogía, fundamentalmente,
la propuesta del griego Spyros Kalomitsines (Kalomitsines, 1985) en su trabajo Some New Ways of Proceeding in Problem Solving, que ahora puede encontrarse en la red. Presentaba el "method of description” y el "getting out of loops" para ayudar a
salir de los bloqueos en los problemas.
En
esta entrada os propongo el problema enunciado en la parte superior, que ejemplifica esta situación y que
recogí del libro de Martin Gardner Nuevos
pasatiempos matemáticos (Gardner, 1972, p. 46). Dejo algunas pistas por si
alguien se atreve con el problema y referencias bibliográficas que podrían ser
consultadas después del esfuerzo.
 |
| Solución generalizada entre los resolutores de todas las edades y que evidencia el bloqueo ante el problema. |
Blanco,
L.J. (1993). Consideraciones elementales
sobre la Resolución de Problemas. Badajoz. Universitas Editorial. (En la pestaña superior: Libros y capítulos de libros).
Blanco,
L.J. (1993). Una clasificación de problemas matemáticos. Épsilon, nº 25, 49-60. (En la pestaña superior: Artículos)
Gardner,
M. (1972). Nuevos pasatiempos matemáticos. Madrid. Alianza.
 |
| Una observación a tener en cuenta |

No hay comentarios:
Publicar un comentario