Un problema de geometría y álgebra, a
través de la manipulación y el lenguaje simbólico.
En
dos entradas anteriores proponíamos actividades matemáticas con palillos sobre
igualdades numéricas con números romanos y sobre orientación en el plano.
Ahora
nos adentramos en la búsqueda de algún patrón para ver cuántos palillos
necesitaremos para construir polígonos.
En nuestro caso, vamos a proponer la
construcción de cuadriláteros.
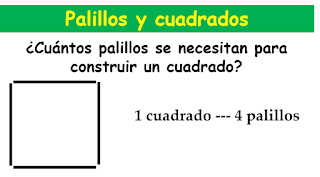
La
primera propuesta es fácil ¿cuántos palillos se necesitan para construir un
cuadrado?
La
segunda, puede tener más de una respuesta y, también, es fácil ¿cuántos palillos
se necesitan para construir dos cuadrados?
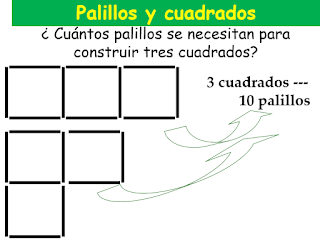
Pero
podemos seguir indagando en el número de palillos que se necesitarán para
construir tres, cuatro, … cuadrados.
Cuando planteamos construir cuadrados podríamos precisar si los cuadrados a construir tienen que ser iguales o no y precisar que se busca el número mínimo de palillos necesarios. En cualquier caso, siempre es interesante que este debate surja en la resolución del problema.
Podemos generalizar el problema, quedando enunciado de la siguiente manera:
Construir cuatro cuadrados con palillos
No hay comentarios:
Publicar un comentario